728x90
피보나치 수 알고리즘
피보나치 수열이란?
첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열
- 위키백과
피보나치 수 F(n)는 다음과 같은 초기값 및 점화식 으로 정의되는 수열이다.
0번째 항부터 시작할 경우 다음과 같이 정의된다.
- 즉 아래와 같이 정의할 수 있다.
- fibo(n) = n == 0 || n == 1 ? n : fibo(n-1) + fibo(n-2)
5가지의 알고리즘
- 코드들은 모두 자바로 작성할 예정입니다.
기본 재귀적 풀이
- 가장 구현하기 쉬운 풀이입니다.
- 가장 큰 단점은 시간복잡도 인데요. 함수가 한 번 호출되면 다시 두 번 호출 되기 때문에 지수적으로 증가하여 O(2^n)이 됩니다.
public static int fibo(final int n) {
if (n >= 2) {
return fibo(n - 1) + fibo(n - 2);
}
return n;
}반복적 풀기
- 0부터 계속 반복해서 앞으로 전지해 나가면서 해당 피포나치 수에 도달하는 방법
- 시간복잡도는 O(n)
public static int fibo(final int n) {
if (n < 2) {
return n;
}
int a = 0;
int b = 1;
for (int i = 0; i < n; i++) {
final int c = (a + b);
a = b;
b = c;
}
return a;
}동적 계획법
- 재귀로 풀엇을 경우 부분 문제가 중복이 된다.
- 부분문제가 너무 많이 중복된다는 것은 각 부분문제를 해결할 때 마다 그것을 저장하고 필요할때 마다 가져다 쓰면 되지 않을까?
- 이러한 동적 계획법 방법은 재귀와 반복적 풀이 두개가 있다.
- 반복적 동적 풀이법
- 부분문제의 답을 계산할 캐시의 형태나 타입은 문제의 특성에 따라 다양하게 설정이 가능하지만, 피보나치 수같은 경우에는 1차원 배열이면 충분하다.
public static int fibo(final int n) {
if (n < 2) {
return n;
}
final int[] cache = new int[n + 1];
cache[1] = 1;
for (int i = 2; i < cache.length; i++) {
cache[i] = cache[i - 1] + cache[i - 2];
}
return cache[n];
}- 재귀적 동적 계획법 풀이
public class FibonacciNumbers {
private static int[] cache;
public static int solution(final int n) {
cache = new int[n + 1];
return fibo(n);
}
public static int fibo(final int n) {
if (n < 2) {
return n;
}
if (cache[n] > 0) {
return cache[n];
}
cache[n] = fibo(n - 1) + fibo(n - 2);
return cache[n];
}
}- 이때 까장 중요한건 더 이상 재귀 함수를 호출하지 않고 끝날 조건을 설정해주는 것으로 이걸 기저사례(base case)라고 부른다.
- 기저사례는 n이 2미만일때와 원하는 부분을 이미 해결했을때로 설정하였다.
행렬 곱셈을 활용한 풀기
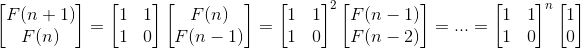
- 위와 같이 피보나치 수를 행렬로 나타낼수 있다.
- 이 방법은 시간복잡도 O(log n)을 가지게 된다.
- 아래가 피보나치 수열의 일반항이다.
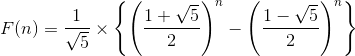
public static int fibo(final int n) {
final double sqrt = Math.sqrt(5);
return (int)(1 / sqrt * (Math.pow((1 + sqrt) / 2, n) - Math.pow((1 - sqrt) / 2, n)));
}참고자료
728x90
728x90
'Common > ComputerScience' 카테고리의 다른 글
| 1부터 100까지 더하는 효율적인 방법 찾기 (0) | 2020.12.27 |
|---|---|
| Permutation Algorithm(순열 알고리즘) & Combination Algorithm(조합 알고리즘) (0) | 2020.12.23 |
| Greedy Algorithms(탐욕 알고리즘) (0) | 2020.12.21 |
| 힙(heap) 알고리즘 이란? (0) | 2020.12.13 |
| Stack vs Queue (0) | 2020.11.18 |
728x90
피보나치 수 알고리즘
피보나치 수열이란?
첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열
- 위키백과
피보나치 수 F(n)는 다음과 같은 초기값 및 점화식 으로 정의되는 수열이다.
0번째 항부터 시작할 경우 다음과 같이 정의된다.
- 즉 아래와 같이 정의할 수 있다.
- fibo(n) = n == 0 || n == 1 ? n : fibo(n-1) + fibo(n-2)
5가지의 알고리즘
- 코드들은 모두 자바로 작성할 예정입니다.
기본 재귀적 풀이
- 가장 구현하기 쉬운 풀이입니다.
- 가장 큰 단점은 시간복잡도 인데요. 함수가 한 번 호출되면 다시 두 번 호출 되기 때문에 지수적으로 증가하여 O(2^n)이 됩니다.
public static int fibo(final int n) {
if (n >= 2) {
return fibo(n - 1) + fibo(n - 2);
}
return n;
}반복적 풀기
- 0부터 계속 반복해서 앞으로 전지해 나가면서 해당 피포나치 수에 도달하는 방법
- 시간복잡도는 O(n)
public static int fibo(final int n) {
if (n < 2) {
return n;
}
int a = 0;
int b = 1;
for (int i = 0; i < n; i++) {
final int c = (a + b);
a = b;
b = c;
}
return a;
}동적 계획법
- 재귀로 풀엇을 경우 부분 문제가 중복이 된다.
- 부분문제가 너무 많이 중복된다는 것은 각 부분문제를 해결할 때 마다 그것을 저장하고 필요할때 마다 가져다 쓰면 되지 않을까?
- 이러한 동적 계획법 방법은 재귀와 반복적 풀이 두개가 있다.
- 반복적 동적 풀이법
- 부분문제의 답을 계산할 캐시의 형태나 타입은 문제의 특성에 따라 다양하게 설정이 가능하지만, 피보나치 수같은 경우에는 1차원 배열이면 충분하다.
public static int fibo(final int n) {
if (n < 2) {
return n;
}
final int[] cache = new int[n + 1];
cache[1] = 1;
for (int i = 2; i < cache.length; i++) {
cache[i] = cache[i - 1] + cache[i - 2];
}
return cache[n];
}- 재귀적 동적 계획법 풀이
public class FibonacciNumbers {
private static int[] cache;
public static int solution(final int n) {
cache = new int[n + 1];
return fibo(n);
}
public static int fibo(final int n) {
if (n < 2) {
return n;
}
if (cache[n] > 0) {
return cache[n];
}
cache[n] = fibo(n - 1) + fibo(n - 2);
return cache[n];
}
}- 이때 까장 중요한건 더 이상 재귀 함수를 호출하지 않고 끝날 조건을 설정해주는 것으로 이걸 기저사례(base case)라고 부른다.
- 기저사례는 n이 2미만일때와 원하는 부분을 이미 해결했을때로 설정하였다.
행렬 곱셈을 활용한 풀기
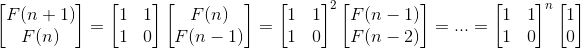
- 위와 같이 피보나치 수를 행렬로 나타낼수 있다.
- 이 방법은 시간복잡도 O(log n)을 가지게 된다.
- 아래가 피보나치 수열의 일반항이다.
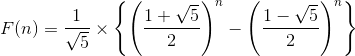
public static int fibo(final int n) {
final double sqrt = Math.sqrt(5);
return (int)(1 / sqrt * (Math.pow((1 + sqrt) / 2, n) - Math.pow((1 - sqrt) / 2, n)));
}참고자료
728x90
728x90
'Common > ComputerScience' 카테고리의 다른 글
| 1부터 100까지 더하는 효율적인 방법 찾기 (0) | 2020.12.27 |
|---|---|
| Permutation Algorithm(순열 알고리즘) & Combination Algorithm(조합 알고리즘) (0) | 2020.12.23 |
| Greedy Algorithms(탐욕 알고리즘) (0) | 2020.12.21 |
| 힙(heap) 알고리즘 이란? (0) | 2020.12.13 |
| Stack vs Queue (0) | 2020.11.18 |




