Permutation Algorithm(순열 알고리즘) & Combination Algorithm(조합 알고리즘)
전체적인 코드는 Java코드로 작성합니다.
순열 알고리즘이란?
수학에서 순열(Permutation) 또는 치환은 순서가 부여된 임의의 집합을 다른 순서로 뒤섞는 연산이다. 즉, 순열은 정의역과 공역이 같은 일대일 대응이다. n개의 원소의 순서를 뒤섞는 순열의 개수는 n의 계승 n!와 같다. 즉, n 이하의 양의 정수들을 곱한 값이다.
-위키피디아
- 공식(nPr)
- 서로 다른 n개중에 r개를 선택하는 경우의 수
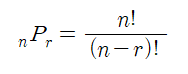
- 모든 경우의 수를 계산하는 완전 탐색에서 사용하는 알고리즘입니다.
- 순서 n개에 대한 모든 경우의 수를 구하는 것은 n!로 구하기 쉽습니다.
- 예를들어 {1, 2, 3}이 있다고 했을때 가능한 경우의 수는 아래와 같습니다.
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1- 위와 같이 순서에 구분이 있습니다. 즉, 1 2 3과 1 3 2는 다른 값이라고 보고 있습니다.
- 중복순열과 그냥 순열은 자기 자신을 포함하는지에 대해 달라집니다.
- 예를들어 {1,2,3}에서 2개를 뽑는 경우의 수는 아래와 같습니다.(순열)
1 2
1 3
2 1
2 3
3 1
3 2- 그러나 중복순열은 자기 자신을 포함하고 있기 때문에 아래와 같이 나오게 됩니다.
1 1
1 2
1 3
2 2
2 1
2 3
3 3
3 1
3 2순열 구현(재귀)
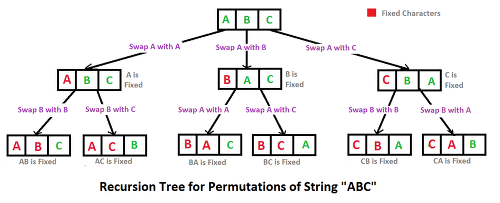
- 위의 사진처럼 재귀적으로 푸는 방법이 존재합니다.
- 다음과 같은 시그니쳐를 사용하면 됩니다.
perm(int[] arr, int depth, int n, int k)
- arr
- 데이터를 교환되고 있는 배열
- depth
- 위의 트리 구조에서 어떤 깊이에서 교환작업을 하고 잇는지에 대한 변수
- n
- 배열안에 들어있는 숫자로 고정값으로 위의 사진에서는 3으로 고정되어 있다.
- k
- 몇개를 뽑아내서 순열을 만들것인가이다.
- 현재 같은 경우는 3개를 뽑아서 3개 모두 사용해 순열하기 때문에 3으로 고정되어 있다.
swap 방식
import java.util.Arrays;
public class Perm {
public static void main(String[] args) {
int[] arr = {1, 2, 3};
perm(arr, 0, arr.length, arr.length);
}
public static void perm(int[] arr, int depth, int n, int r) {
if (depth == r) { // 한번의 depth가 k로 도달하면 사이클을 한번 돈거다.)
System.out.println(Arrays.toString(arr));
return;
}
for (int i = depth; i < n; i++) {
swap(arr, i, depth);
perm(arr, depth + 1, n, r);
swap(arr, i, depth);
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}완전탐색에서 순열 알고리즘 사용하기
- 예를들어 {1, 2, 3}이 있을때 아래와 같이 결과를 얻고 싶을수도 있다.
1
2
3
12
21
13
31
23
32
123
132
213
231
312
321- 위와 같은 결과는 어떻게 얻을수 있는지에 대해서는 아래 코드에서 살펴보자
import java.util.LinkedList;
public class Perm {
public static void main(String[] args) {
int[] arr = {1, 2, 3};
int n = arr.length;
for (int i = 1; i <= n; i++) {
LinkedList<Integer> perArr = new LinkedList<>();
int[] perCheck = new int[n];
permutation(n, i, perArr, perCheck, arr);
}
}
private static void permutation(int n, int r, LinkedList<Integer> perArr, int[] perCheck, int[] arr) {
if (perArr.size() == r) {
for (int i : perArr) {
System.out.print(i + " ");
}
System.out.println();
return;
}
for (int i = 0; i < n; i++) {
if (perCheck[i] == 0) {
perArr.add(arr[i]); //값을 넣는 부분
perCheck[i] = 1;
permutation(n, r, perArr, perCheck, arr);
perCheck[i] = 0;
perArr.removeLast();
}
}
}
}중복 순열 구현
import java.util.LinkedList;
public class Perm {
public static void main(String[] args) {
int[] arr = {1, 2, 3};
int n = arr.length;
int r = 2;
//중복순열 (순서있게 배열 + 자기 자신도 포함)
System.out.println("\n중복순열");
LinkedList<Integer> rePerArr = new LinkedList<>();
rePermutation(n, r, rePerArr, arr);
}
//중복순열 (순서있게 배열 + 자기 자신도 포함)
private static void rePermutation(int n, int r, LinkedList<Integer> rePerArr, int[] arr) {
if (rePerArr.size() == r) {
for (int i : rePerArr) {
System.out.print(i + " ");
}
System.out.println();
return;
}
for (int i = 0; i < n; i++) {
rePerArr.add(arr[i]);
rePermutation(n, r, rePerArr, arr);
rePerArr.removeLast();
}
}
}Combination Algorithm(조합 알고리즘)
집합에서 서로 다른 n개의 원소 중에서 순서에 상관없이 r개를 선택하는 것이다.
위키 피디아
순열과 다른 점은 순서에 구분이 없습니다. 즉, 1 2 3과 1 3 2는 같은 값이라고 바라보기 때문에 하나의 결과만 나오게 됩니다.
1 2 3
1 2 4
1 3 4
2 3 4예를들어 {1,2,3,4}이 있다면 가능한 경우의 수는 아래와 같습니다.
공식(nCr)
서로 다른 n개 중에 r개를 선택하는 경우의 수
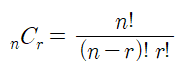
조합 알고리즘 구현
import java.util.LinkedList;
public class Perm {
public static void main(String[] args) {
int[] arr = {1, 2, 3};
int n = arr.length;
//조합 (순서 관심 없고 뽑은 유무만 생각)
System.out.println("\n조합");
for (int i = 1; i <= n; i++) {
int[] comArr = new int[i];
combination(comArr, n, i, 0, 0, arr);
}
}
//조합 (순서 관심 없고 뽑은 유무만 생각)
private static void combination(int[] comArr, int n, int r, int index, int target, int[] arr) {
if (r == 0) {
for (int i : comArr) {
System.out.print(i + " ");
}
System.out.println();
return;
}
if (target == n) {
return;
}
comArr[index] = arr[target];
combination(comArr, n, r - 1, index + 1, target + 1, arr); //뽑는 경우
combination(comArr, n, r, index, target + 1, arr); //안 뽑는 경우
}
}중복조합 코드
import java.util.LinkedList;
public class Perm {
public static void main(String[] args) {
int[] arr = {1, 2, 3};
int n = arr.length;
//중복 조합 (순서 관심 없고 뽑은 유무만 생각 + 자기 자신도 포함)
System.out.println("\n중복조합");
for (int i = 0; i <= n; i++) {
int[] reComArr = new int[i];
reCombination(reComArr, n, i, 0, 0, arr);
}
}
//중복 조합 (순서 관심 없고 뽑은 유무만 생각 + 자기 자신도 포함)
private static void reCombination(int[] reComArr, int n, int r, int index, int target, int[] arr) {
if (r == 0) {
for (int i : reComArr) {
System.out.print(i + " ");
}
System.out.println();
return;
}
if (target == n)
return;
reComArr[index] = arr[target];
reCombination(reComArr, n, r - 1, index + 1, target, arr);//뽑는 경우
reCombination(reComArr, n, r, index, target + 1, arr);//안 뽑는 경우
}
}전체 코드
import java.util.LinkedList;
public class Perm {
public static void main(String[] args) {
int[] arr = {1, 2, 3};
int n = arr.length;
//순열 (순서있게 배열)
System.out.println("\n 순열");
for (int i = 1; i <= n; i++) {
LinkedList<Integer> perArr = new LinkedList<>();
int[] perCheck = new int[n];
permutation(n, i, perArr, perCheck, arr);
}
//중복순열 (순서있게 배열 + 자기 자신도 포함)
System.out.println("\n중복순열");
for (int i = 1; i <= n; i++) {
LinkedList<Integer> rePerArr = new LinkedList<>();
rePermutation(n, i, rePerArr, arr);
}
//조합 (순서 관심 없고 뽑은 유무만 생각)
System.out.println("\n조합");
for (int i = 1; i <= n; i++) {
int[] comArr = new int[i];
combination(comArr, n, i, 0, 0, arr);
}
//중복 조합 (순서 관심 없고 뽑은 유무만 생각 + 자기 자신도 포함)
System.out.println("\n중복조합");
for (int i = 0; i <= n; i++) {
int[] reComArr = new int[i];
reCombination(reComArr, n, i, 0, 0, arr);
}
}
//순열(순서있게 배열)
private static void permutation(int n, int r, LinkedList<Integer> perArr, int[] perCheck, int[] arr) {
if (perArr.size() == r) {
for (int i : perArr) {
System.out.print(i + " ");
}
System.out.println();
return;
}
for (int i = 0; i < n; i++) {
if (perCheck[i] == 0) {
perArr.add(arr[i]); //값을 넣는 부분
perCheck[i] = 1;
permutation(n, r, perArr, perCheck, arr);
perCheck[i] = 0;
perArr.removeLast();
}
}
}
//중복순열 (순서있게 배열 + 자기 자신도 포함)
private static void rePermutation(int n, int r, LinkedList<Integer> rePerArr, int[] arr) {
if (rePerArr.size() == r) {
for (int i : rePerArr) {
System.out.print(i + " ");
}
System.out.println();
return;
}
for (int i = 0; i < n; i++) {
rePerArr.add(arr[i]);
rePermutation(n, r, rePerArr, arr);
rePerArr.removeLast();
}
}
//조합 (순서 관심 없고 뽑은 유무만 생각)
private static void combination(int[] comArr, int n, int r, int index, int target, int[] arr) {
if (r == 0) {
for (int i : comArr) {
System.out.print(i + " ");
}
System.out.println();
return;
}
if (target == n) {
return;
}
comArr[index] = arr[target];
combination(comArr, n, r - 1, index + 1, target + 1, arr); //뽑는 경우
combination(comArr, n, r, index, target + 1, arr); //안 뽑는 경우
}
//중복 조합 (순서 관심 없고 뽑은 유무만 생각 + 자기 자신도 포함)
private static void reCombination(int[] reComArr, int n, int r, int index, int target, int[] arr) {
if (r == 0) {
for (int i : reComArr) {
System.out.print(i + " ");
}
System.out.println();
return;
}
if (target == n)
return;
reComArr[index] = arr[target];
reCombination(reComArr, n, r - 1, index + 1, target, arr);//뽑는 경우
reCombination(reComArr, n, r, index, target + 1, arr);//안 뽑는 경우
}
}참고자료
'Common > ComputerScience' 카테고리의 다른 글
| DFS(Depth First Search) VS BFS(Breadth First Search) (0) | 2020.12.28 |
|---|---|
| 1부터 100까지 더하는 효율적인 방법 찾기 (0) | 2020.12.27 |
| Greedy Algorithms(탐욕 알고리즘) (0) | 2020.12.21 |
| 피보나치 수 알고리즘 (0) | 2020.12.14 |
| 힙(heap) 알고리즘 이란? (0) | 2020.12.13 |
Permutation Algorithm(순열 알고리즘) & Combination Algorithm(조합 알고리즘)
전체적인 코드는 Java코드로 작성합니다.
순열 알고리즘이란?
수학에서 순열(Permutation) 또는 치환은 순서가 부여된 임의의 집합을 다른 순서로 뒤섞는 연산이다. 즉, 순열은 정의역과 공역이 같은 일대일 대응이다. n개의 원소의 순서를 뒤섞는 순열의 개수는 n의 계승 n!와 같다. 즉, n 이하의 양의 정수들을 곱한 값이다.
-위키피디아
- 공식(nPr)
- 서로 다른 n개중에 r개를 선택하는 경우의 수
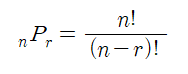
- 모든 경우의 수를 계산하는 완전 탐색에서 사용하는 알고리즘입니다.
- 순서 n개에 대한 모든 경우의 수를 구하는 것은 n!로 구하기 쉽습니다.
- 예를들어 {1, 2, 3}이 있다고 했을때 가능한 경우의 수는 아래와 같습니다.
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1- 위와 같이 순서에 구분이 있습니다. 즉, 1 2 3과 1 3 2는 다른 값이라고 보고 있습니다.
- 중복순열과 그냥 순열은 자기 자신을 포함하는지에 대해 달라집니다.
- 예를들어 {1,2,3}에서 2개를 뽑는 경우의 수는 아래와 같습니다.(순열)
1 2
1 3
2 1
2 3
3 1
3 2- 그러나 중복순열은 자기 자신을 포함하고 있기 때문에 아래와 같이 나오게 됩니다.
1 1
1 2
1 3
2 2
2 1
2 3
3 3
3 1
3 2순열 구현(재귀)

- 위의 사진처럼 재귀적으로 푸는 방법이 존재합니다.
- 다음과 같은 시그니쳐를 사용하면 됩니다.
perm(int[] arr, int depth, int n, int k)
- arr
- 데이터를 교환되고 있는 배열
- depth
- 위의 트리 구조에서 어떤 깊이에서 교환작업을 하고 잇는지에 대한 변수
- n
- 배열안에 들어있는 숫자로 고정값으로 위의 사진에서는 3으로 고정되어 있다.
- k
- 몇개를 뽑아내서 순열을 만들것인가이다.
- 현재 같은 경우는 3개를 뽑아서 3개 모두 사용해 순열하기 때문에 3으로 고정되어 있다.
swap 방식
import java.util.Arrays;
public class Perm {
public static void main(String[] args) {
int[] arr = {1, 2, 3};
perm(arr, 0, arr.length, arr.length);
}
public static void perm(int[] arr, int depth, int n, int r) {
if (depth == r) { // 한번의 depth가 k로 도달하면 사이클을 한번 돈거다.)
System.out.println(Arrays.toString(arr));
return;
}
for (int i = depth; i < n; i++) {
swap(arr, i, depth);
perm(arr, depth + 1, n, r);
swap(arr, i, depth);
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}완전탐색에서 순열 알고리즘 사용하기
- 예를들어 {1, 2, 3}이 있을때 아래와 같이 결과를 얻고 싶을수도 있다.
1
2
3
12
21
13
31
23
32
123
132
213
231
312
321- 위와 같은 결과는 어떻게 얻을수 있는지에 대해서는 아래 코드에서 살펴보자
import java.util.LinkedList;
public class Perm {
public static void main(String[] args) {
int[] arr = {1, 2, 3};
int n = arr.length;
for (int i = 1; i <= n; i++) {
LinkedList<Integer> perArr = new LinkedList<>();
int[] perCheck = new int[n];
permutation(n, i, perArr, perCheck, arr);
}
}
private static void permutation(int n, int r, LinkedList<Integer> perArr, int[] perCheck, int[] arr) {
if (perArr.size() == r) {
for (int i : perArr) {
System.out.print(i + " ");
}
System.out.println();
return;
}
for (int i = 0; i < n; i++) {
if (perCheck[i] == 0) {
perArr.add(arr[i]); //값을 넣는 부분
perCheck[i] = 1;
permutation(n, r, perArr, perCheck, arr);
perCheck[i] = 0;
perArr.removeLast();
}
}
}
}중복 순열 구현
import java.util.LinkedList;
public class Perm {
public static void main(String[] args) {
int[] arr = {1, 2, 3};
int n = arr.length;
int r = 2;
//중복순열 (순서있게 배열 + 자기 자신도 포함)
System.out.println("\n중복순열");
LinkedList<Integer> rePerArr = new LinkedList<>();
rePermutation(n, r, rePerArr, arr);
}
//중복순열 (순서있게 배열 + 자기 자신도 포함)
private static void rePermutation(int n, int r, LinkedList<Integer> rePerArr, int[] arr) {
if (rePerArr.size() == r) {
for (int i : rePerArr) {
System.out.print(i + " ");
}
System.out.println();
return;
}
for (int i = 0; i < n; i++) {
rePerArr.add(arr[i]);
rePermutation(n, r, rePerArr, arr);
rePerArr.removeLast();
}
}
}Combination Algorithm(조합 알고리즘)
집합에서 서로 다른 n개의 원소 중에서 순서에 상관없이 r개를 선택하는 것이다.
위키 피디아
순열과 다른 점은 순서에 구분이 없습니다. 즉, 1 2 3과 1 3 2는 같은 값이라고 바라보기 때문에 하나의 결과만 나오게 됩니다.
1 2 3
1 2 4
1 3 4
2 3 4예를들어 {1,2,3,4}이 있다면 가능한 경우의 수는 아래와 같습니다.
공식(nCr)
서로 다른 n개 중에 r개를 선택하는 경우의 수
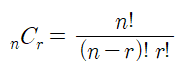
조합 알고리즘 구현
import java.util.LinkedList;
public class Perm {
public static void main(String[] args) {
int[] arr = {1, 2, 3};
int n = arr.length;
//조합 (순서 관심 없고 뽑은 유무만 생각)
System.out.println("\n조합");
for (int i = 1; i <= n; i++) {
int[] comArr = new int[i];
combination(comArr, n, i, 0, 0, arr);
}
}
//조합 (순서 관심 없고 뽑은 유무만 생각)
private static void combination(int[] comArr, int n, int r, int index, int target, int[] arr) {
if (r == 0) {
for (int i : comArr) {
System.out.print(i + " ");
}
System.out.println();
return;
}
if (target == n) {
return;
}
comArr[index] = arr[target];
combination(comArr, n, r - 1, index + 1, target + 1, arr); //뽑는 경우
combination(comArr, n, r, index, target + 1, arr); //안 뽑는 경우
}
}중복조합 코드
import java.util.LinkedList;
public class Perm {
public static void main(String[] args) {
int[] arr = {1, 2, 3};
int n = arr.length;
//중복 조합 (순서 관심 없고 뽑은 유무만 생각 + 자기 자신도 포함)
System.out.println("\n중복조합");
for (int i = 0; i <= n; i++) {
int[] reComArr = new int[i];
reCombination(reComArr, n, i, 0, 0, arr);
}
}
//중복 조합 (순서 관심 없고 뽑은 유무만 생각 + 자기 자신도 포함)
private static void reCombination(int[] reComArr, int n, int r, int index, int target, int[] arr) {
if (r == 0) {
for (int i : reComArr) {
System.out.print(i + " ");
}
System.out.println();
return;
}
if (target == n)
return;
reComArr[index] = arr[target];
reCombination(reComArr, n, r - 1, index + 1, target, arr);//뽑는 경우
reCombination(reComArr, n, r, index, target + 1, arr);//안 뽑는 경우
}
}전체 코드
import java.util.LinkedList;
public class Perm {
public static void main(String[] args) {
int[] arr = {1, 2, 3};
int n = arr.length;
//순열 (순서있게 배열)
System.out.println("\n 순열");
for (int i = 1; i <= n; i++) {
LinkedList<Integer> perArr = new LinkedList<>();
int[] perCheck = new int[n];
permutation(n, i, perArr, perCheck, arr);
}
//중복순열 (순서있게 배열 + 자기 자신도 포함)
System.out.println("\n중복순열");
for (int i = 1; i <= n; i++) {
LinkedList<Integer> rePerArr = new LinkedList<>();
rePermutation(n, i, rePerArr, arr);
}
//조합 (순서 관심 없고 뽑은 유무만 생각)
System.out.println("\n조합");
for (int i = 1; i <= n; i++) {
int[] comArr = new int[i];
combination(comArr, n, i, 0, 0, arr);
}
//중복 조합 (순서 관심 없고 뽑은 유무만 생각 + 자기 자신도 포함)
System.out.println("\n중복조합");
for (int i = 0; i <= n; i++) {
int[] reComArr = new int[i];
reCombination(reComArr, n, i, 0, 0, arr);
}
}
//순열(순서있게 배열)
private static void permutation(int n, int r, LinkedList<Integer> perArr, int[] perCheck, int[] arr) {
if (perArr.size() == r) {
for (int i : perArr) {
System.out.print(i + " ");
}
System.out.println();
return;
}
for (int i = 0; i < n; i++) {
if (perCheck[i] == 0) {
perArr.add(arr[i]); //값을 넣는 부분
perCheck[i] = 1;
permutation(n, r, perArr, perCheck, arr);
perCheck[i] = 0;
perArr.removeLast();
}
}
}
//중복순열 (순서있게 배열 + 자기 자신도 포함)
private static void rePermutation(int n, int r, LinkedList<Integer> rePerArr, int[] arr) {
if (rePerArr.size() == r) {
for (int i : rePerArr) {
System.out.print(i + " ");
}
System.out.println();
return;
}
for (int i = 0; i < n; i++) {
rePerArr.add(arr[i]);
rePermutation(n, r, rePerArr, arr);
rePerArr.removeLast();
}
}
//조합 (순서 관심 없고 뽑은 유무만 생각)
private static void combination(int[] comArr, int n, int r, int index, int target, int[] arr) {
if (r == 0) {
for (int i : comArr) {
System.out.print(i + " ");
}
System.out.println();
return;
}
if (target == n) {
return;
}
comArr[index] = arr[target];
combination(comArr, n, r - 1, index + 1, target + 1, arr); //뽑는 경우
combination(comArr, n, r, index, target + 1, arr); //안 뽑는 경우
}
//중복 조합 (순서 관심 없고 뽑은 유무만 생각 + 자기 자신도 포함)
private static void reCombination(int[] reComArr, int n, int r, int index, int target, int[] arr) {
if (r == 0) {
for (int i : reComArr) {
System.out.print(i + " ");
}
System.out.println();
return;
}
if (target == n)
return;
reComArr[index] = arr[target];
reCombination(reComArr, n, r - 1, index + 1, target, arr);//뽑는 경우
reCombination(reComArr, n, r, index, target + 1, arr);//안 뽑는 경우
}
}참고자료
'Common > ComputerScience' 카테고리의 다른 글
| DFS(Depth First Search) VS BFS(Breadth First Search) (0) | 2020.12.28 |
|---|---|
| 1부터 100까지 더하는 효율적인 방법 찾기 (0) | 2020.12.27 |
| Greedy Algorithms(탐욕 알고리즘) (0) | 2020.12.21 |
| 피보나치 수 알고리즘 (0) | 2020.12.14 |
| 힙(heap) 알고리즘 이란? (0) | 2020.12.13 |