728x90
힙(heap)알고리즘 이란?
서론
- 자료구조로 완전 이진 트리의 일종으로 우선순위 큐를 위해 만들어진 자료구조다.
- 여러 개의 값들 중 최댓값, 최솟값을 빠르게 찾아내도록 만들어진 자료구조
- 힙 트리에서는 중복된 값을 허용한다. (이진 탐색 트리에서는 중복된 값을 허용하지 않는다.)
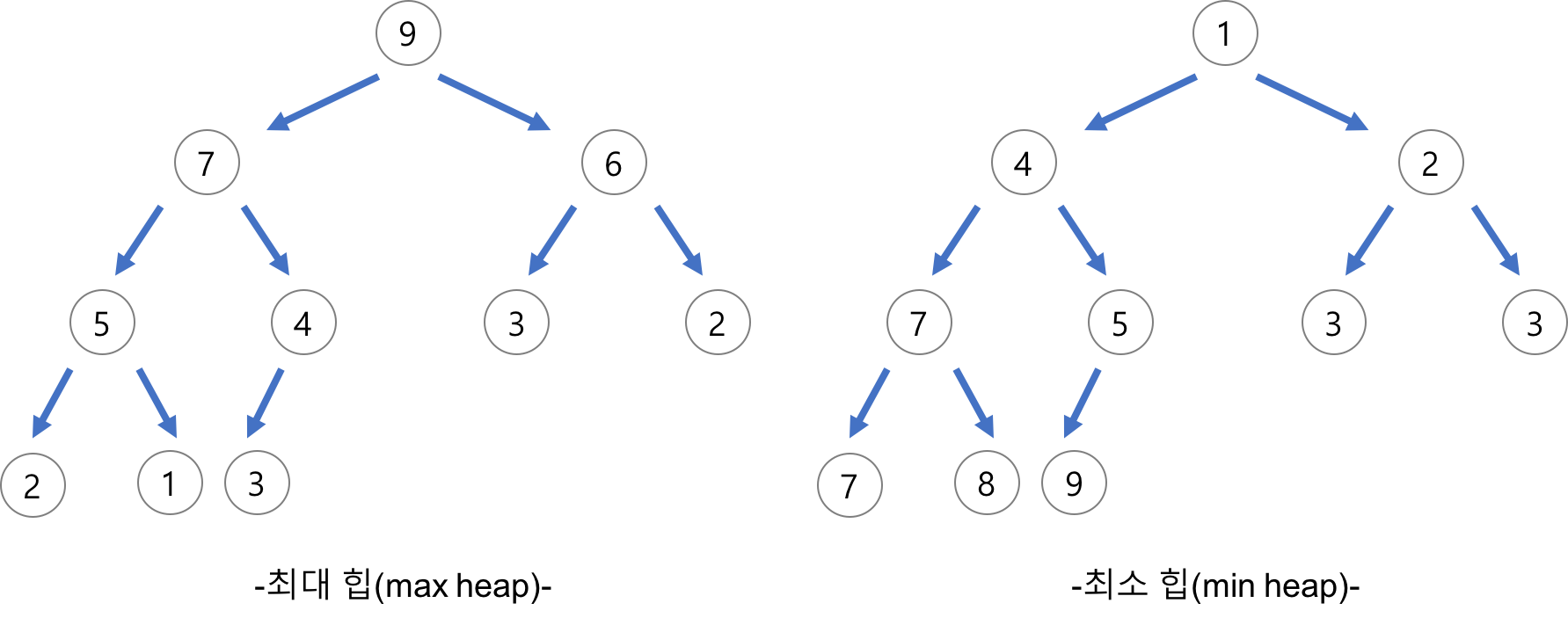
힙의 종류
- 최대 힙
- 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
- 부모 노드 ≥ 자식노드
- 최소 힙
- 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
- 부모 노드 ≤ 자식노드
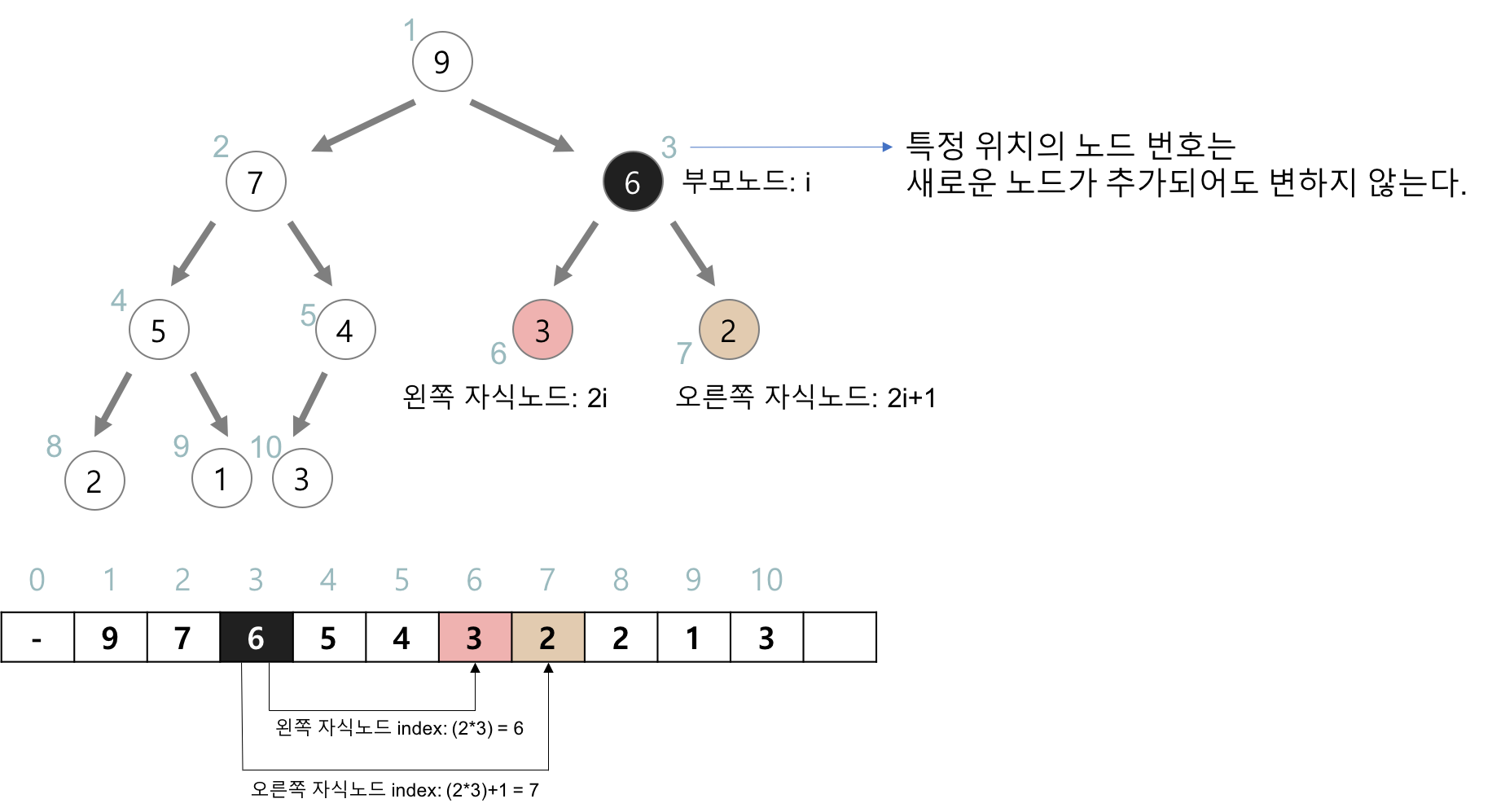
힙의 구현
- 힙을 저장하는 표준적인 자료구조는 배열
- 구현을 쉽게 하기 위해 첫번째 인덱스는 사용되지 않는다.
- 특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않는다.
- 힙에서의 부모 노드와 자식 노드의 관계
- 왼쪽 자식의 노드 = (부모의 인덱스) * 2
- 오른쪽 자식의 노드 = (부모의 인덱스) * 2 + 1
- 부모의 인덱스 = (자식의 인덱스) / 2
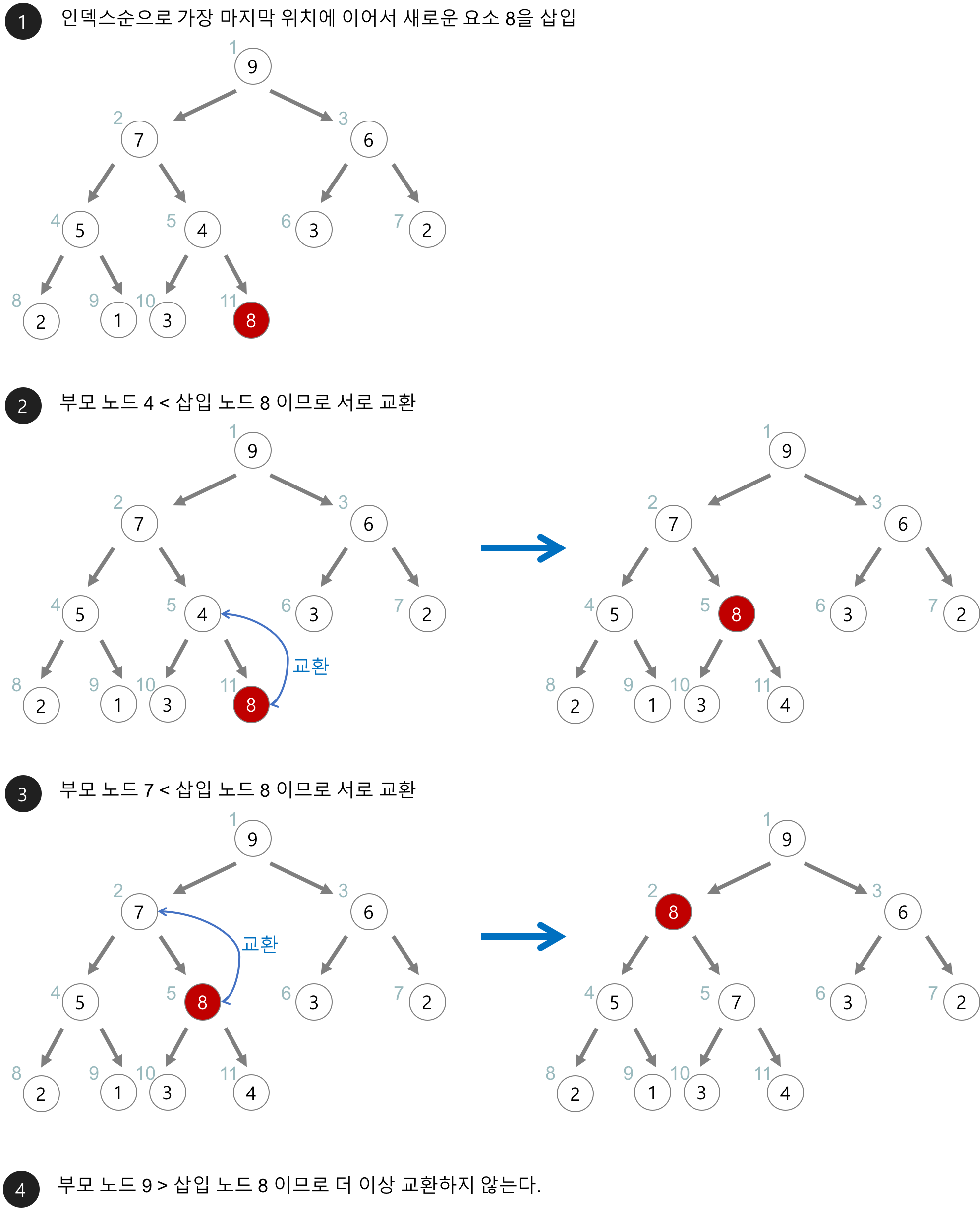
삽입
- 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다.
- 새로운 노드를 부모 노드들과 교환하여 힙의 성질(최소, 최대)의 성질을 만족시킨다.
- 힙의 있는 노드의 개수를 n이라고 할때 O(n)의 시간이 걸린다.
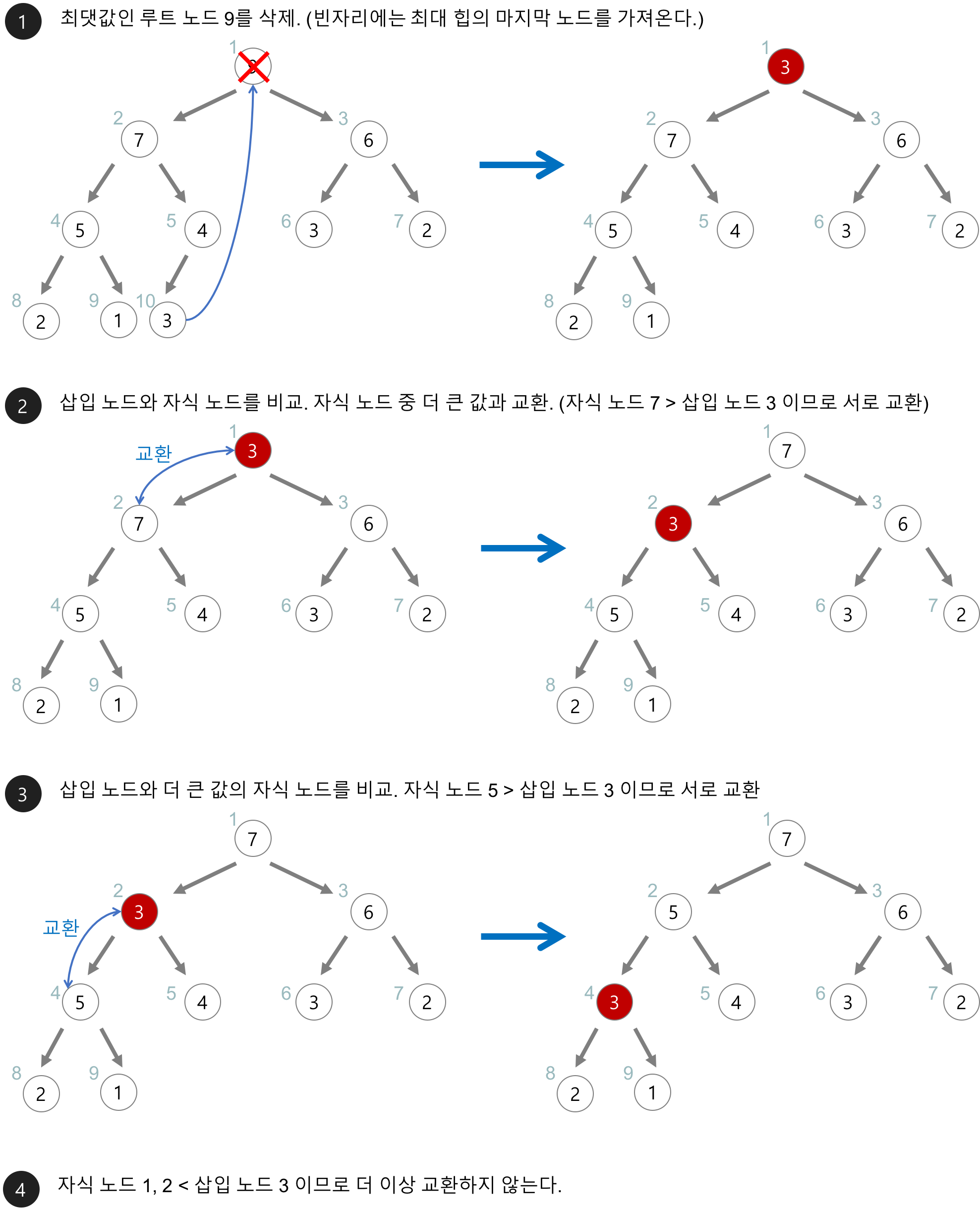
힙의 삭제
- 최대값이나 최소값은 루트 노드이기때문에 루트 노드를 삭제합니다.
- 최소 원소를 제거한 후에 힙에 있는 가장 마지막 원소와 교환
- 해당 노드를 자식 노드와 교환해 나가면서 밑으로 내보낸다.
- 힙의 있는 노드의 개수를 n이라고 할때 O(n)의 시간이 걸린다.
MaxHeap With Java
public class MaxHeap {
private final int[] heap;
private final int maxSize;
private int size;
public MaxHeap(final int maxSize) {
this.maxSize = maxSize;
this.size = 0;
heap = new int[maxSize + 1];
heap[0] = Integer.MAX_VALUE;
}
public static void main(final String[] args) {
final MaxHeap maxHeap = new MaxHeap(15);
maxHeap.insert(5);
maxHeap.insert(3);
maxHeap.insert(17);
maxHeap.insert(10);
maxHeap.insert(84);
maxHeap.insert(19);
maxHeap.insert(6);
maxHeap.insert(22);
maxHeap.insert(9);
System.out.println(maxHeap.extractMax());
}
private static int parent(final int position) {
return position / 2;
}
private static int leftChild(final int position) {
return position * 2;
}
private static int rightChild(final int position) {
return position * 2 + 1;
}
private boolean isLeaf(final int position) {
return position >= size / 2 && position <= size;
}
private void swap(final int firstPosition, final int secondPosition) {
final int temp = heap[firstPosition];
heap[firstPosition] = heap[secondPosition];
heap[secondPosition] = temp;
}
private void maxHeapify(final int position) {
if (isLeaf(position)) {
return;
}
if (heap[position] < heap[leftChild(position)] || heap[position] < heap[rightChild(position)]) {
if (heap[leftChild(position)] > heap[rightChild(position)]) {
swap(position, leftChild(position));
maxHeapify(leftChild(position));
} else {
swap(position, rightChild(position));
maxHeapify(position);
}
}
}
private void insert(final int elemnet) {
heap[++size] = elemnet;
int current = size;
while (heap[current] > heap[parent(current)]) {
swap(current, parent(current));
current = parent(current);
}
}
public int extractMax() {
final int poped = heap[1];
heap[1] = heap[--size];
maxHeapify(1);
return poped;
}
}PriorityQueue
- 자바는 이미 우선순위큐를 구현하고 있습니다.
- MinHeap으로 되어 있으며 아래와 같이 사용하면 됩니다.
PriorityQueue<Integer> pQueue =
new PriorityQueue<Integer>();- MaxHeap을 사용하려면 아래와 같이 하시면 됩니다.
PriorityQueue<Integer> pQueue =
new PriorityQueue<Integer>(Collections.reverseOrder());결론
- 알고리즘 문제에서 Heap 관련되어 있는 문제들은 자바로 풀때 모두 PriorityQueue로 손쉽게 풀 수 있습니다.
- 그러나 어떻게 구현이 되어서 내부에서 어떤 로직으로 되어가는지는 꼭 알아야 한다고 생각합니다.
참고자료
728x90
728x90
'Common > ComputerScience' 카테고리의 다른 글
| 1부터 100까지 더하는 효율적인 방법 찾기 (0) | 2020.12.27 |
|---|---|
| Permutation Algorithm(순열 알고리즘) & Combination Algorithm(조합 알고리즘) (0) | 2020.12.23 |
| Greedy Algorithms(탐욕 알고리즘) (0) | 2020.12.21 |
| 피보나치 수 알고리즘 (0) | 2020.12.14 |
| Stack vs Queue (0) | 2020.11.18 |
728x90
힙(heap)알고리즘 이란?
서론
- 자료구조로 완전 이진 트리의 일종으로 우선순위 큐를 위해 만들어진 자료구조다.
- 여러 개의 값들 중 최댓값, 최솟값을 빠르게 찾아내도록 만들어진 자료구조
- 힙 트리에서는 중복된 값을 허용한다. (이진 탐색 트리에서는 중복된 값을 허용하지 않는다.)
힙의 종류
- 최대 힙
- 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
- 부모 노드 ≥ 자식노드
- 최소 힙
- 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 완전 이진 트리
- 부모 노드 ≤ 자식노드

힙의 구현
- 힙을 저장하는 표준적인 자료구조는 배열
- 구현을 쉽게 하기 위해 첫번째 인덱스는 사용되지 않는다.
- 특정 위치의 노드 번호는 새로운 노드가 추가되어도 변하지 않는다.
- 힙에서의 부모 노드와 자식 노드의 관계
- 왼쪽 자식의 노드 = (부모의 인덱스) * 2
- 오른쪽 자식의 노드 = (부모의 인덱스) * 2 + 1
- 부모의 인덱스 = (자식의 인덱스) / 2

삽입
- 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다.
- 새로운 노드를 부모 노드들과 교환하여 힙의 성질(최소, 최대)의 성질을 만족시킨다.
- 힙의 있는 노드의 개수를 n이라고 할때 O(n)의 시간이 걸린다.

힙의 삭제
- 최대값이나 최소값은 루트 노드이기때문에 루트 노드를 삭제합니다.
- 최소 원소를 제거한 후에 힙에 있는 가장 마지막 원소와 교환
- 해당 노드를 자식 노드와 교환해 나가면서 밑으로 내보낸다.
- 힙의 있는 노드의 개수를 n이라고 할때 O(n)의 시간이 걸린다.

MaxHeap With Java
public class MaxHeap {
private final int[] heap;
private final int maxSize;
private int size;
public MaxHeap(final int maxSize) {
this.maxSize = maxSize;
this.size = 0;
heap = new int[maxSize + 1];
heap[0] = Integer.MAX_VALUE;
}
public static void main(final String[] args) {
final MaxHeap maxHeap = new MaxHeap(15);
maxHeap.insert(5);
maxHeap.insert(3);
maxHeap.insert(17);
maxHeap.insert(10);
maxHeap.insert(84);
maxHeap.insert(19);
maxHeap.insert(6);
maxHeap.insert(22);
maxHeap.insert(9);
System.out.println(maxHeap.extractMax());
}
private static int parent(final int position) {
return position / 2;
}
private static int leftChild(final int position) {
return position * 2;
}
private static int rightChild(final int position) {
return position * 2 + 1;
}
private boolean isLeaf(final int position) {
return position >= size / 2 && position <= size;
}
private void swap(final int firstPosition, final int secondPosition) {
final int temp = heap[firstPosition];
heap[firstPosition] = heap[secondPosition];
heap[secondPosition] = temp;
}
private void maxHeapify(final int position) {
if (isLeaf(position)) {
return;
}
if (heap[position] < heap[leftChild(position)] || heap[position] < heap[rightChild(position)]) {
if (heap[leftChild(position)] > heap[rightChild(position)]) {
swap(position, leftChild(position));
maxHeapify(leftChild(position));
} else {
swap(position, rightChild(position));
maxHeapify(position);
}
}
}
private void insert(final int elemnet) {
heap[++size] = elemnet;
int current = size;
while (heap[current] > heap[parent(current)]) {
swap(current, parent(current));
current = parent(current);
}
}
public int extractMax() {
final int poped = heap[1];
heap[1] = heap[--size];
maxHeapify(1);
return poped;
}
}PriorityQueue
- 자바는 이미 우선순위큐를 구현하고 있습니다.
- MinHeap으로 되어 있으며 아래와 같이 사용하면 됩니다.
PriorityQueue<Integer> pQueue =
new PriorityQueue<Integer>();- MaxHeap을 사용하려면 아래와 같이 하시면 됩니다.
PriorityQueue<Integer> pQueue =
new PriorityQueue<Integer>(Collections.reverseOrder());결론
- 알고리즘 문제에서 Heap 관련되어 있는 문제들은 자바로 풀때 모두 PriorityQueue로 손쉽게 풀 수 있습니다.
- 그러나 어떻게 구현이 되어서 내부에서 어떤 로직으로 되어가는지는 꼭 알아야 한다고 생각합니다.
참고자료
728x90
728x90
'Common > ComputerScience' 카테고리의 다른 글
| 1부터 100까지 더하는 효율적인 방법 찾기 (0) | 2020.12.27 |
|---|---|
| Permutation Algorithm(순열 알고리즘) & Combination Algorithm(조합 알고리즘) (0) | 2020.12.23 |
| Greedy Algorithms(탐욕 알고리즘) (0) | 2020.12.21 |
| 피보나치 수 알고리즘 (0) | 2020.12.14 |
| Stack vs Queue (0) | 2020.11.18 |